결로 현상에 대해 완벽히 이해하고, 방지하기 (feat. 이슬점 계산기).

안녕하세요.
오늘 깊이 생각할 주제는 바로 '결로(結맺을 결 露이슬 로)(Dew condensation)'입니다. 사전적 정의는 '이슬이 맺힘' 정도가 되겠죠. 24절기의 백로, 한로란 이름도 해가 지면서 기온이 낮아져 발생하는 이슬에 의해 유래되었습니다.
하지만 밖에서 발생하는 이슬이 실내에서 발생한다면, 이건 문제가 있겠죠?! 우리가 인식하는 실내에서 발생하는 결로란 각종 곰팡이가 번식할 수 있는 환경을 만들어주는 현상입니다. 심한 경우, 본격적으로 날이 쌀쌀해지는 늦가을부터 나타나기도 합니다.

이 포스팅을 통해 많은 분들이 결로에서 해방되기를 기원하며, 본격적인 내용을 작성해보겠습니다. 기초적인 개념부터 차근차근히 시작할 것이기 때문에 이미 다 아는 내용이 있거나, 시간적 여유가 없으신 분들께서는 현재 당장 필요한 내용만 참고하시면 되겠습니다. 해당 포스팅은 수식으로 인해, PC에 최적화 되어있으니 참고하시기 바랍니다.

그리고 이슬점 계산기는 본 포스팅 최하단에 위치해있습니다. 계산만 필요하신 분은 곧장 밑으로 가시면 됩니다.

---

결로는 간단하게만 보면, 공기 중 기체 상태의 물인 수증기가 차가운 표면에 맺혀 액체 상태의 물이 되는 것입니다. 그러면 먼저 어떤 요인이 이를 가능하게 하는지를 알아봐야 하겠습니다.
증기압(Vapor pressure) 또는 평형증기압(Equilibrium vapor pressure) 또는 포화증기압(Saturated vapor pressure)이라는 개념이 필수적으로 필요합니다.
모든 응축 상태에 있는 어떤 물질(액체 또는 고체)은 기체 상태로 되려는 성질이 있습니다. 물을 가만히 놔두면 증발(Vaporization)이라는 현상이 일어난다는 것은 경험적으로 알고 계실 겁니다. 물뿐만이 아니라 모든 물질이 이러한 성질을 띄고 있는데요. 여기서 다음과 같은 질문을 하나 던질 수 있습니다.

"과연 언제까지 기체가 될 수 있을까?"

이를 설명할 수 있는 개념이 증기압입니다. 그리고 증기압, 평형증기압, 포화증기압 모두 정확히 동일한 개념입니다. 표현이 달라 서로 다른 개념으로 받아들일 수 있는데요. 약간의 상상을 통해 동일하다는 것을 알 수 있습니다. 증기압을 어떻게 측정할 것인지에 대해 생각을 해보면 쉽습니다.
어떤 액체의 증기압을 측정하려고 하는 사람은 과연 어떻게 증기압을 측정할까요?! 액체에서 실시간으로 뿜어져 나오는 증기의 압력을 바로바로 측정할 수 있을까요?! 아마, 불가능할 것입니다.

이제부터 자세히 설명을 해드리겠습니다. 일반적으로 증발을 설명할 때 다음과 같은 그림을 많이 사용합니다.

어떤 계면을 중심으로 액체 그리고 기체의 상(Phase)이 있는 닫힌 계를 간략히 표현해봤습니다. 아래가 액체 상태이고, 위가 기체 상태입니다. 같은 면적의 계면에 검은 화살표와 하늘색 화살표의 수가 다르죠. 화살표의 수는 계면에서 다른 상 쪽으로 행하는 힘의 세기로 이해하시면 편합니다. 면적이 같은데 힘이 다르니 압력의 차이가 발생하는 것이죠.

다시 말해, 액체에서 기체가 되는 녀석들이 기체에서 액체로 되는 녀석들보다 더 많다는 것을 의미합니다. 결국 겉보기 변화로는 점점 액체가 기체 상태로 되는 것으로 보입니다. 기체에서 액체가 되는 녀석들이 있음에도 불구하고 말이죠. 그리고 점차 시간이 지나면, 아래와 같은 그림을 보게 될 것입니다.

포화(Saturation) 상태가 되었군요. 이 상태를 평형(Equilibrium) 상태라고도 합니다.계면에서 행하는 힘이 서로 같아졌으므로, 겉보기 변화도 사라졌을 것입니다. 이제 증기압을 측정하려고 하는 사람은 기체가 존재하는 위 부분에 측정기를 장착해 압력을 측정하겠죠?!
액체가 기체가 되려는 증기압은 처음부터 끝까지 변한 것이 하나도 없습니다. 단순히 현재의 계가 포화되었을 뿐이죠. 그리고 이렇게 포화가 되어야만 측정이 실제로 가능해진다는 것입니다. 그래서 그냥 증기압이 평형증기압이자 포화증기압이라는 것입니다.
그런데, 위 그림들은 엄밀히 말해서, 올바르지 않다고 생각합니다. 조금 이상하지 않나요?! 위 그림에서 액체, 기체 상태에 있는 분자들의 수가 똑같아졌습니다. 분자들의 수가 같아졌으면 똑같이 액체이거나 기체여야 하지 않을까요?! 어떤 상태의 차이를 나누는 개념인, 계면이라는 것이 존재하지 않는 상황인 것이죠.
그래서 제 생각에 더 정확한 상황을 묘사하는 그림을 그려봤습니다.

액체는 기체보다 어마어마하게 밀도가 크므로, 액체 상태의 분자들은 나타내지 않고 색을 칠해버렸습니다. 그리고 액체 표면 아주 가까이에 정확한 두께는 알 수 없지만(아주 얇을 것이라 상상합니다) 항상 액체와 평형을 유지하는(항상 포화 상태인) 층이 있다고 생각을 해봤습니다. 그리고 실질적으로 이 영역에 있는 기체가 앞서 약간 올바르지 않은 액체(?)와 같은 역할을 하는 것이죠. 실제 중요한 계면은 아래 그림처럼 이동을 하게 되는 것이고요.

사실, 단순히 액체와 증발되는 공간 사이에 상상의 영역을 추가한 것에 지나지 않습니다. 저는 액체 상태의 분자들은 표현할 필요가 없다고 생각이 들었습니다. 액체는 기체와 다르게 분자 간의 인력이 상상을 초월할 정도로 세기도 하고, 특히나 그걸 시각적으로 표현할 길이 없으니까요. 그래서 액체 층은 분자들을 저 얇은 층에 끊임 없이 공급해주는 공급원의 역할만 할 뿐인 것으로 받아들이기로 했습니다. 어차피 액체의 성질은 저 영역에 있는 기체 분자들이 '대변'해줄 것입니다.

저는 이렇게 상상을 하니, 증발 및 증기압이란 개념이 더욱 더 이해하기 쉬워지더군요. 만약 이 개념이 말이 되지 않는다고 생각하시어 댓글로 반박해주셔도 겸허히 수용하겠습니다.

그리고 동일 물질의 증기압은 온도에만 의존하는 것으로 알려져 있습니다. 온도가 올라가면, 증기압도 올라갑니다. 온도가 높아지면 저 항상 평형을 유지하는 얇은 층에 액체로부터 단위 시간 당 더 많은 분자들이 공급된다고 생각하시면 될 것 같습니다. 어쨌든 증기압에 대한 설명은 여기서 마치기로 하겠습니다.
이제부터는 직관적일 수 있도록 '포화증기압'으로만 언급하겠습니다.
자, 그럼 포화증기압이 온도에 따라 달라진다고 했는데, 물의 포화증기압은 어떻게 달라질까요?

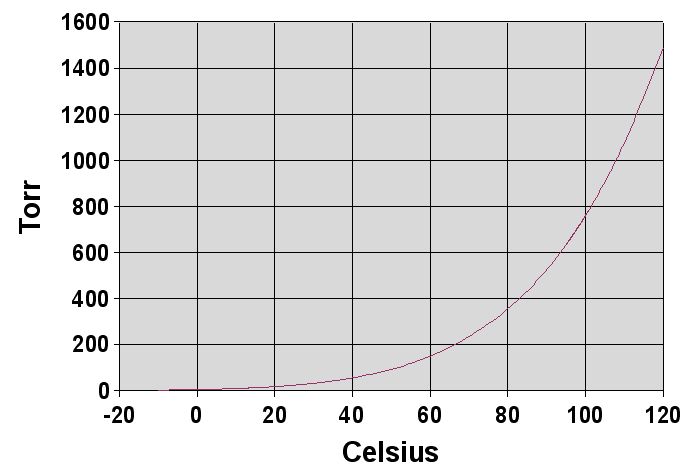
Reference: Wikipedia

측정 결과는 위처럼 지수함수 형태를 보여주고 있습니다. 이 결과를 설명할 수 있는 Equation을 얻기 위해 많은 분들이 노력하셨습니다. 그 중에 저는 Buck Equation을 여러분들께 소개해드릴 겁니다. 왜냐하면 1℃ 단위로 포화증기압을 기록한 표를 찾기가 귀찮기도 하고, 0℃부터 100℃까지 무려 101줄이나 잡아먹기 때문입니다. 그리고 이 녀석이 아주 꽤 정확하거든요. 그리고 정확히 해를 찾을 수도 있습니다. Buck Equation은 다음과 같습니다.

\[P = 0.61121 \exp{[(\frac{18.678 - T}{234.5})(\frac{T}{257.14 + T})]}\] \[P: \text { pressure}, \quad T: \text{ temperature}\]
온도 \(T\)는 ℃단위를 사용하시면 되고, 결과인 포화증기압 \(P\)의 단위는 kPa입니다. 약간은 복잡하지만, 뭐.. 괜찮습니다. 이 공식으로 결로가 생기는 상황을 계산할 것입니다.

마지막으로 아주 중요한 개념이 상대 습도(Relative humidity)라는 개념입니다. 상대 습도의 정의는 다음과 같습니다.

\[RH = \frac { p_\mathrm{ H_2O } }{ p^* _\mathrm{ H_2O } }\] \[RH: \text { relative humidity}, \quad p_\mathrm{ H_2O }: \text{ partial pressure of water vapor}, \quad p^*_\mathrm{ H_2O }: \text{ vapor pressure of water}\]
어느 특정 온도에서 대기 중의 수증기 분압을 포화증기압으로 나눠준 값입니다. 많은 곳에서 물의 '양'을 도입해서 설명하는데 저는 이것이 더 엄밀한 정의라 생각이 됩니다. 왜냐하면 압력이 가장 최초로 측정되는 물리량이기 때문입니다. 상대 습도와 물의 포화증기압 및 그의 분압에 대해 간단한 예시를 들어 더 쉽게 설명해드리겠습니다. 아까 얘기해드린 것처럼 물 아주 가까이 근처에는 항상 포화 상태인 층이 존재를 하고, 여기 있는 수증기가 항상 포화증기압만큼 외부로 압력을 가합니다(물론 물 쪽으로도). 그리고 외부에 있는 수증기도 이 항상 포화 상태인 층 또는 물 쪽으로 어떤 압력을 가하겠죠.
만약에 외부의 수증기가 물 쪽으로 포화증기압과 동일한 압력을 가한다면?! 그것은 현재 그 닫힌 계가 포화 상태라는 것을 의미합니다. 왜냐하면 압력을 가한다는 것은 수증기가 압력을 가하는 방향으로 이동한다는 것이니까요. 그런데 이 압력이 같다는 뜻은 항상 포화 상태인 층에서 나가는 수증기와 외부에서 들어오는 수증기의 양이 똑같아서 액체의 물에서 수증기를 공급 받을 필요가 없기 때문입니다. 이때가 바로 상대 습도 100%라고 얘기할 수 있는 것입니다. 물은 전혀 건조되지 않겠죠. 만약 상대 습도가 50%라면, 외부에서 가해지는 수증기의 압력이 포화증기압의 절반이라는 뜻이겠지요. 열린 계 상태에서 상대 습도가 100% 미만이기만 하면, 물은 언젠가 다 증발합니다. 그래서 사실 건조에서 제일 중요한 것은 온도가 아니라 습도입니다. 습식 사우나를 상상해보세요. 온도가 엄청 높지만 물방울이 떠다니는 것이 보일 정도로 높은 습도를 자랑하죠. 이곳에서는 빨래가 전혀 마르지 않습니다.
즉, 외부에 존재하는 수증기만의 압력(수증기의 분압)과 포화증기압과의 비율이 상대 습도입니다.
자, 상대 습도도 설명이 끝났습니다. 이제 결로 방지를 위한 과학적 개념을 다 터득하셨습니다.

빠른 진행을 위해 실내의 물의 포화증기압을 포화수증기압, 실내 대기의 수증기 분압을 수증기압으로 언급하겠습니다. 지금까지 제가 설명해드린 개념을 다 이해하셨다면!
결로는 실내 대기의 수증기압이, 결로가 발생하는 부분의 포화수증기압을 넘어가기 시작하면 발생한다는 것을 아셔야 합니다.
"어?! 결로가 발생하는 부분에는 애초에 물이 없는데 무슨 포화수증기압이야?!"고 하실 수도 있습니다. 그래서 제가 Saturation Region을 위에서 도입한 것입니다. 간단한 개념이지만 물이 만들어질 수밖에 없겠구나라는 생각이 들게 만들기 위해서요. 수증기 자체가 차가운 부분에 닿으면서 포화가 되고 결국 Saturation Region이 생겨나고 액체의 물이 발생합니다.
즉, 온도가 결정되면 물이 있든 없든, 그 온도에 일치하는 포화수증기압이 가상적으로(?) 하지만 필수적으로 존재한다고 생각해주셔야 합니다.
어쨌든 물이 생겨났다면, 이 물은 실내 내부 온도보다 훨씬 차가운 곳에 있기 때문에 어떠한 추가 대처 없이는 이 부근의 포화수증기압은 실내 대기의 수증기압보다 계속 낮은 상태로 있게 되고, 점점 물은 줄줄 흐르게 되겠죠.

하지만 희망은 있습니다.

결로라는 것이 무조건 온도 차이가 존재한다고 해서 발생하는 것이 아니거든요. 가장 중요한 것은 실질적인 수증기의 겉보기 이동을 일으키는 압력의 차이니까요.
바로 이것이 핵심입니다. 그 임계 온도를 찾아내는 것이 이 포스팅의 목표입니다.
그러면 본격적으로 시작해보겠습니다.

결로 발생에 영향을 주는 변수는 실내의 온도(\(T_R\)), 실내의 상대 습도(\(RH\)), 결로가 우려되는 곳의 온도(\(T\))로 총 3개가 되겠습니다(포화수증기압은 온도가 결정되면 알아서 결정되는 것이고, 수증기압은 상대 습도를 이용해 계산을 할 수 있으니까요).
결로를 막기 위해서는 다음과 같이 3가지 방법을 생각할 수가 있습니다.

1. 내가 \(T_R\)을 알고 \(RH\)를 알고 있을 때, \(T\)를 결로가 발생하지 않는 온도로 만드는 법.
2. 내가 \(T\)를 알고 \(RH\)를 알고 있을 때, \(T_R\)를 결로가 발생하지 않는 온도로 만드는 법.
3. 내가 \(T_R\)을 알고 \(T\)를 알고 있을 때, \(RH\)를 결로가 발생하지 않는 습도로 만드는 법.

자, 어떤 것이 합리적인 방법일까요?!
실제로 \(T\)를 알기 위해서는 결로 발생 지점의 표면 온도를 측정해야 합니다. '적외선 온도계'가 필요해요. 삼겹살 파는 식당에서 불판 온도 잴 때 쓰는 그 물건 아시죠?! 혹시, 이거 갖고 계시는 분들이 많으실까요?! 저는 없습니다만, 그리 비싸지는 않으니 관심이 있다면 구매하는 것을 추천해드립니다. 보유하고 있으면 여러 방면에 도움이 될 것 같습니다. 그리고 \(T_R\)과 \(RH\)는 온도계, 습도계가 집에 있다면 당연히 바로 알 수 있겠죠?!
온도계가 없다면, 방에 있는 '보일러 조작기(?)'를 참고하시면 됩니다. '실내 온도' 모드로 바꾸면 온도가 출력이 되는데 이 기기 내부에 온도 센서가 탑재되어 있다고 해요. 또는 요새 공기 청정기에도 온도계, 습도계 기능이 탑재되어 있던데 이것을 참고하셔도 되고요. 습도 조절 가능 제습기가 있다면 이것으로 습도를 파악하시면 되겠습니다. 사실, 제 추천이지만 제습기가 있으면 정말 좋습니다. 왜냐하면, 요새 미세먼지 때문에 창문 열어 습도 낮추기가 너무 힘들거든요. 그리고 에어컨의 제습 기능은 습도 기준이 아닌, 온도 기준으로 제습을 하기 때문에 겨울철에 사용하기 많이 어렵습니다. 무엇보다 가동하면 더 추워지니..;;
제습기는 확실히 날이 추워질 때 그리고 요즘처럼 미세먼지가 기승을 부릴 때 사용하면 삶의 질이 향상되는 가전제품이라고 생각합니다.

어쨌거나 드디어 Buck Equation을 이용할 시간입니다. 우리는 해답이 나오는 상황을 이제 알고 있습니다. 실내 대기의 수증기압이 결로가 우려되는 부분의 포화수증기압을 넘어서면 안된다는 것입니다.
즉, 아래의 조건을 만족해야 합니다.

\[RH\times P^*_R < P_\mathrm{ROI}\] \[P_\mathrm{ROI}: \text{ vapor pressure of ROI }, \quad P^*_R: \text{ vapor pressure of water in room}\] \[\text{ROI: region of interest}\]
두 값이 정확히 같아질 때는 어떻게 될까요?! 아주 간당간당한 상황인 거죠. 약간의 흔들림만으로도 이슬이 맺히거나, 안 맺히거나!
이 경계의 온도를 이슬점(Dew point)이라고 부릅니다. 이슬이 맺히기 시작하는 온도를 말하는 것이죠. 우리는 결로 우려 지점의 온도가 이슬점보다 높으면 문제가 없는 것이고, 낮으면 문제가 있는 겁니다.
그럼 계속해서 이슬점을 유도해보도록 하겠습니다. 위 부등식에서 부등호를 그냥 등호(\(=\))로 바꿔주기만 하면, 이슬점을 구할 수 있습니다.
마지막으로 정리하자면, 이슬점이란 바로 결로 우려 지점의 포화수증기압이 현재 주어진 실내 수증기압과 같아질 수 있는 '그 지점의 온도'가 바로 이슬점(\(T_D\))입니다.

\[\begin{align} P_\mathrm{ROI} &= RH \times P^*_R \\ &= RH \times 0.61121 \exp{[(\frac{18.678 - T_R}{234.5})(\frac{T_R}{257.14 + T_R})]} \\ &= 0.61121 \exp{[(\frac{18.678 - T_D}{234.5})(\frac{T_D}{257.14 + T_D})]} \end{align}\] \[T_R: \text{ temperature of room }, \quad T_D: \text{ dew point of ROI}\]
어떻게 처음에 풀어야할지만 언급하고 자세한 과정은 생략하겠습니다. 일단 Equation에 포함되어 있는 수치들은 치환을 해줄 것입니다. 그렇지 않으면 미친 듯이 지저분한 결과를 얻거든요.

\[a=18.678, b=234.5, c=257.14\]
그리고 위 식 양변에 자연로그 \(\ln\)을 취한 후 잘 풀면 됩니다. 일단 자연로그를 취한 결과는 다음과 같습니다.

\[\ln RH + (a - \frac{T_R}{b})(\frac{T_R}{c+T_R}) = (a - \frac{T_D}{b})(\frac{T_D}{c+T_D})\]
그리고 대망의 결과, \(T_D\)는 아래와 같이 얻어집니다.

\[\therefore T_D = \frac{T_R^2 + abc - b (\ln RH)(c + T_R) - \sqrt{(T_R^2 + abc - b (\ln RH)(c + T_R))^2 + 4c(c + T_R)(T_R^2 - abT_R - b (\ln RH)(c + T_R))}}{2(c + T_R)}\]
위 결과는 전혀 어려운 것이 아닙니다. 그냥 복잡한 것입니다. 이렇게 방정식을 풀지 않으면, 저희는 3가지 변수를 모조리 Split해서 노가다(?) 작업을 무진장 많이 해야 합니다. 물론 이 노가다는 그냥 숫자를 때려 넣는 것이기 때문에 결과는 수많은 테이블이고 그 테이블에서 이슬점을 직접 찾아내야 합니다. 그리고 이 정리 자료는 이슬점을 검색하시면 그 값들이 모조리 들어가있는 테이블로 많이 돌아다닙니다. 어쨌든, 우리는 이슬점 계산을 위해 이 식에 원래 들어가있던 수 \(a\), \(b\), \(c\)를 대입해주고, 실내에서 측정한 \(T_R\), \(RH\)를 넣어주면 됩니다.

자, 이렇게 \(T_D\)를 구하면 무엇이 좋을까요?
우리가 실내의 온도, 습도를 원하는 정도로 맞추고 난 후, 결로 발생이 우려되는 곳이 실제로 문제가 발생하는가의 파악이 쉬워집니다. 이것이 무슨 말이냐면, 겨울철에 권장되는 실내 온도, 습도가 있습니다. 온도는 18-20℃, 습도는 40-60% 범위를 유지하는 것이 건강에 좋다고 합니다. 겨울철에도 우리가 건강한 실내 생활을 하기 위해 유지해야만 하는 최소 조건입니다. 일단 먼저 이 값들 내에서 실내 조건을 고정하고, 결로 발생의 유무를 일단 확인해보자는 것입니다.
이 범위 내에서 생활하고 있는데 결로가 생긴다면?! 그제서야 바로 단열 시공의 불량을 지적할 수가 있게 되는 것입니다.
물론, 시공 업체 또는 건물주에서 이를 받아들이느냐는 또 다른 문제이긴 하죠.
하지만 우리는 모든 것에 대해 잘 알아야 할 필요가 있습니다. 확실한 증거들을 제시해야 합니다.

그러면, 이제 저 겨울철 적정 범위에서 결로가 생기는 \(T_D\)를 구해보겠습니다. 20℃, 60% 습도에서 가장 높은 \(T_D\)가 약 12.01℃로 계산되며, 18℃, 40% 습도에서 가장 낮은 \(T_D\)가 약 4.21℃로 얻어집니다.
즉, 겨울철에 실내의 어떤 표면의 온도를 측정했을 때 4.21℃ 이하의 온도가 측정된다면, 권장되는 실내 최소 조건을 유지한 채로는 결로를 막지 못한다는 결론이 도출됩니다.
저는 사실 온도는 조금 더 낮아도 무조건 습도는 거의 55%를 유지했을 때 쾌적함을 느낍니다. 55% 미만일 때는 호흡기 쪽이 많이 건조해짐을 느끼기 때문입니다. 그래서 저는 습도만큼은 포기하지 않는 방향을 추구합니다(60%도 좋지만, 약간 습함이 느껴지고, 결로의 위험성도 조금 더 올라가기 때문입니다). 저만의 겨울철 실내 조건의 마지노선은 16℃에 55%입니다. 이때 이슬점은 6.97℃입니다. 사실 요새 웬만한 이중창에서는 도달할 수 없는 온도입니다. 만약에 제가 이 조건으로 생활 중임에도 결로가 생기지 않는다면, 저는 실내 온도를 조금 더 올려서 생활할 수 있는 여유가 생기는 것이고(참 다행이겠죠), 결로가 생긴다면, 16℃까지도 충분히 타협을 했다고 생각하는데 그 미만의 온도로 겨울을 버텨라?! 용납할 수 없는 것이죠. 시공의 문제인 것입니다.

저희가 지금까지 구한 해를 통해 마음만 먹으면 엑셀 등을 이용해 온도 1℃ 또는 0.1℃ 간격으로 출력해 거대한 표를 손에 넣을 수도 있습니다만, 이미 dew point table은 시중에 많이 돌아다니기 때문에 이를 참고하시는 것이 더 좋을 것 같습니다.

지금까지 결로의 원리에 대해 알아보고, 실제 이슬점 계산까지 해본 뜻 깊은 포스팅이었습니다. 많은 분들이 결로에서 해방되어 건강한 겨울철 보내셨으면 좋겠습니다. 이상입니다.
감사합니다.

---

Dew Point Calculator(이슬점 계산기)

\(T_R\)(실내 온도)(℃)

\(RH\)(실내 습도)(%)

Dew Point(이슬점)(℃)


사용법: 실내 온도와 실내 습도를 입력해주시고 Calculate!!를 클릭해주시면 됩니다.